These pages use the MathJax package to display mathematical equations, which
uses JavaScript. Leaving scripts disabled will deprive you of seeing any
equation in correct typesetting.
Matematik og regne øvelser (dag 21)
Regler for øvelserne:
Brug papir og blyant . Hvis du ikke kan/vil/gider holde dig til denne regel, så skal du lade være med at deltage;
Brug op til nogenlunde 15..20 minutter på at løse opgaverne/spørgsmålene per dag;
Svarene kan ses dagen efter. Du skal selv kontrollere om du har svaret rigtigt;
Besvar spørgsmålene i den rækkefølge du synes er nemmest;
Du bør anvende strege-metoden hvor hensigtsmæssigt, og omskrive med (kendte) simple regler;
Du bør prøve at løse tal-opgaver uden
Tjek dine resultater dagen efter og se hvor du kan forbedre dig;
Der er mange veje til samme mål. Du skal finde din vej i løbet af øvelserne;
Hvis du har et problem du ikke kan løse eller andet spørgsmål, så send en email til
<forrige dag> 1 ,
2 ,
3 ,
4 ,
5 ,
6 ,
7 ,
8 ,
9 ,
10 ,
11 ,
12 ,
13 ,
14 ,
15 ,
16 ,
17 ,
18 ,
19 ,
20 ,
21
1 , 2 , 3 , 4 , 5 , 6 , 7 , Opgaverne til dag 21
Opgave 1:
\begin{equation}
\frac{15^2}{25} = ?
\end{equation}
Svar 1:
(klik for at vise/skjule)
\(
\frac{15^2}{25}
= \frac{15 \cdot 15}{25}
= \frac{3 \cdot 15}{5}
= \frac{3 \cdot 3}{1}
= \frac{9}{1}
= 9
\)
Tilbage til toppen
Opgave 2:
Hvilke faktorer har \(768\)?
Svar 2:
(klik for at vise/skjule)
\(768/2 = 384\)
Tilbage til toppen
Opgave 3:
\begin{equation}
\frac{15 \cdot 10^{-6}}{12 \cdot 10^{-7}} \cdot 8 \cdot 10^{-4} + 56 \cdot 10^{-3} = ?
\end{equation}
Svar 3:
(klik for at vise/skjule)
\( \frac{15 \cdot 10^{-6}}{12 \cdot 10^{-7}} \cdot 8 \cdot 10^{-4} + 56 \cdot 10^{-3}\)
Tilbage til toppen
Opgave 4:
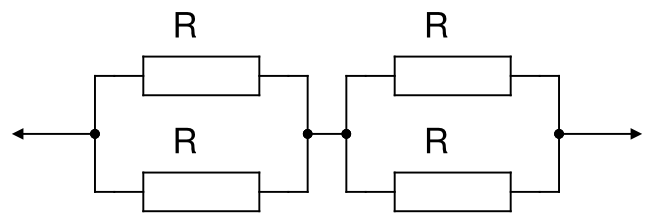
Et kredsløb er lavet med fire modstande som vist i diagrammet. En forrig opgave
har etableret at erstatningens modstanden er \(R\). Hvis hver modstand i
diagrammet kan klare en effekt på \(1\space W\), hvor stor effekt kan det
viste kredsløbet så klare?
Svar 4:
(klik for at vise/skjule)
Fordi alle fire modstande er ens vil både strøm og spænding fordele sig ens
over alle modstande. Det vil sige at effekten for hver modstand er ens. Der er
fire modstande der kan klare \(1 \space W\) hver, så samlet kan de klare
\(4 \cdot 1 \space W = \underline{4 \space W}\).
Tilbage til toppen
Opgave 5:
\begin{equation}
I = \frac{C \cdot U}{t} \Rightarrow U = ?
\end{equation}
Svar 5:
(klik for at vise/skjule)
\(I = \frac{C \cdot U}{t}\)
Tilbage til toppen
Opgave 6:
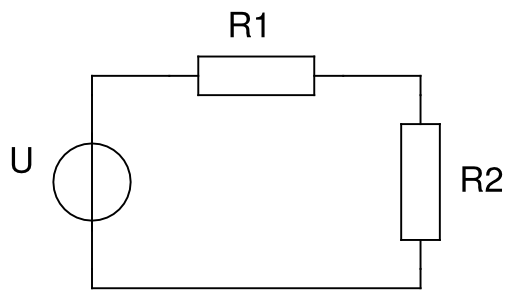
Maksimum effekt teorema
Hvis \(R_1\) og \(U\) er konstant (og større end nul), ved hvad værdi af \(R_2\) er effekten afsat i \(R_2\) maksimal?
Hint: Spænding over \(R_2\) er en spændingsdeler \(U_{R_2} = U \cdot \frac{R_2}{R_1 + R_2}\), og effekten er \(P = U^2/R\).
Note: Denne opgave alene kan tage mere end 15 minutter at løse. Den er ellers en god øvelse.
Svar 6:
(klik for at vise/skjule)
Spænding over \(R_2\) er defineret som en spændingsdeler med \(R_1\) og \(R_2\):
Tilbage til toppen
Opgave 7:
Hor mange opgaver har der været over alle 21 dage i denne regne øvelse?
Svar 7:
(klik for at vise/skjule)
100 opgaver ialt.
Dag Opgaver
1 3
2 3
3 3
4 3
5 4
6 4
7 4
8 4
9 4
10 5
11 5
12 5
13 5
14 5
15 6
16 6
17 6
18 6
19 6
20 6
21 7
-----
100
Tilbage til toppen
<forrige dag> 1 ,
2 ,
3 ,
4 ,
5 ,
6 ,
7 ,
8 ,
9 ,
10 ,
11 ,
12 ,
13 ,
14 ,
15 ,
16 ,
17 ,
18 ,
19 ,
20 ,
21